As research tools in rock deformation have become more sophisticated, we are discovering complexities that are difficult to unravel in standard analytical fashion. In particular, now that we are using synchrotron x-ray diffraction to measure the state state of stress in specimens as they are being deformed, we see unanticipated details of the mesophysics of deformation. We are taking up a new strategy for parting the curtains of ignorance: numerical simulation.

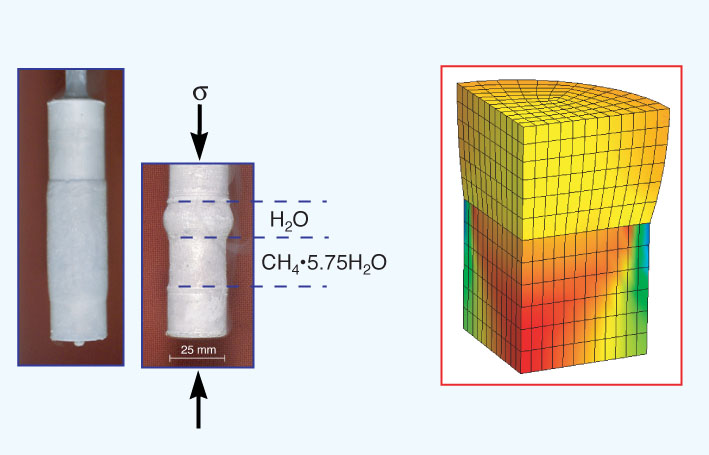
The figure above shows an early attempt to dynamically model flow in a very simple system. The actual sample, deformed in the ice creep rig, is shown at the left. The sample (encapsulated in a gas-tight indium jacket) is actually two discs of materials of widely different strength stacked end for end: ordinary ice on top and methane clathrate hydrate, a much stronger material [see Durham et al., 2003], on the bottom. The numerical simulation in this case is based on a dynamic finite element code. Colors in the simulation indicate the magnitude of the vertical stress, ranging from red, which is near zero, to blue, where the compressive stress is a maximum. Numerical methods show promise for unraveling the very practical problem of complex stress geometries within the sample assembly of the Deformation-DIA. No work has yet been published, as we haven't gotten much farther than the images shown here, but the good new is we have very recently received NSF funding to pursue this modeling [PDF].

Another knotty problem we regularly encounter in the synchrotron relates to the grain-scale physics of deformation of polycrystalline materials (like rocks). The state of stress in a deforming polycrystal varies enormously from grain to grain because the crystals that make up the solid are themselves plastically anisotropic (i.e., they prefer to slip on certain crystallographic planes in certain crystallographic directions). We are blind to this in making the stress measurement macroscopically on the whole sample, as with the ice creep apparatus. X-ray diffraction on the other hand reveals to us the state of stress of individual grains, of which there are thousands in an ordinary sample. For example, in polycrystalline olivine undergoing deformation in the D-DIA, differential stress measured at the (hkl)=(122) diffraction condition that is twice the flow stress measured at (hkl)=(131). So which stress level do we take in applying the experimental result to Earth's mantle? Some of us are turning to numerical methods to solve the problem, in particular, to viscoplastic self-consistent (VPSC) modeling. Again this work is in its infancy, but preliminary efforts are promising [e.g., Chen et al., 2006].